Why Quantum Computing will take another 50 years
This article is meant to be a short, well sourced summary about why we will not have quantum computing any time soon, with evidence that shows we have not made any meaningful progress for decades, at least nowhere near the level the PR lies from the tech industry would have led you to believe.
- The actual challenges for quantum computing
- The current landscape
- Scale of requirements for a real, useful quantum computer
- Conclusion
The actual challenges for quantum computing
For real quantum computing, there are a few parameters that really matter. We are many, many orders of magnitudes away from the level we need to be on each of these parameters when it comes to realizing a real quantum computer that can do meaningful computation. Each category is a Manhattan project level effort (x10) to overcome, and all three need to be overcome, or you have nothing.
Decoherence time
This is how long the entangled state can remain stable/not collapse, and not just when it's doing “nothing”, but when the qubits are actually being operated on and moved through the chip/system. This gets harder the bigger the chip, the more complicated the qubit connectivity structure, and the more qubits that are entangled together. So far no (computationally) meaningful coherence has been achieved for anything other than a few qubits (less than 10).
 |
|---|
| A very simplified visualization of quantum decoherence event |
On top of the state being more fragile by default due to Zeeman/Stark effects and other issues, the larger the number of qubits in a system, the higher the chance that control signals (microwave pulses for superconducting qubits, laser pulses for ions, etc.) interfere with each other due to exponentially increasing crosstalk, worsening decoherence time even more.
Gate fidelity
A “gate” performs logical operations on qubits. For both electrons and photons, gates are not perfect. In isolation, a single gate might show high fidelity (e.g. 99%), but once you try to assemble a large, computation-supporting circuit that involves many gates in parallel, qubit routing, and frequent measurements, the effective error rate quickly climbs (often well past 50%) because every layer of gates and every source of crosstalk compounds. Many published 99% fidelities apply only to contrived demonstrations with few gates under highly controlled conditions, and as such are meaningless in a computation context. Once you entangle a significant number of qubits or shuttle states around, the errors multiply, requiring exponentially greater overhead for error correction.
 |
|---|
| Different quantum circuit topologies. The all-to-all configuration is the hardest to achieve, but even though the others are easier, they introduce additional complexity elsewhere (like needing more gates and more complex control systems) |
Even if you can make small batches of qubits that are very locally stable, and try to “link” them together, large-scale algorithms require qubits to communicate efficiently in a “fully connected” manner. Physical layouts (e.g., 2D arrays in superconducting chips, non-local connections) heavily limit which qubits can directly interact. Swapping states over many “hops” to deal with poor connectivity inflates error even more. Robust long-distance quantum links are far from a solved problem.
Error correction
Because quantum states are noisy generally, and statistical in nature, colossal efforts are required to correct for errors so that the final result actually makes sense rather than being a random distribution. For universal QC, all operations also have to be “reversible”, and compounding error rates destroy that. This means that to actually have stable computation, in a quantum computer that would be able to factor real private keys using Shor, for 1,000-2,000 “logical qubits” you need millions of physical, error correcting qubits.
 |
|---|
| Example circuit that performs a hadamard transform on the one data qubit and its two ancillas (supporting qubits that enable reversible computation), and phase error correction through a Toffoli gate. (source) |
On top of this, error correction schemes (e.g., surface codes) require frequent and precise measurements of ancillary qubits without collapsing computational states. Even with the best error correcting codes, physical gate fidelity has to be below an error threshold of 0.01% to prevent errors from outpacing corrections.
The error correcting overhead for the computation grows exponentially with the number of logical qubits needed, so scaling to even hundreds (much less thousands) of logical qubits is essentially impossible at the moment. There's also a time overhead – a large share of computational cycles are spent on error detection and correction, slowing down actual computation, which then requires greater decoherence time to offset... and so on.
There's no “free lunch”, if you try to cheat by avoiding fully dealing with the problem complexity from one of these 3 areas, you make your life 100x harder when solving for the other 2.
The current landscape
Let's cover what the true state of the art is to set a baseline and recalibrate expectations created by misleading QC press releases.
Some quick background: quantum computers come in 2 main flavors: electronic (manipulating electrons/charged particles), and photonic (manipulating photons, which have no charge).
Electrons are easier to manipulate because they have charge and mass – so they aren't constantly trying to fly into everything at the speed of light – but they are far more susceptible to thermal noise and stray field effects. Photons are more robust to noise, but are harder to control, have greater signal loss and suffer from lower interaction rates, which still mess up your circuits – just in a different way.
The only real qubit “computation” that has ever been done
If you want to perform actually valuable quantum computation that gives you real quantum advantage, you need true, stable and fully entangled qubits – otherwise you cannot run general purpose algorithms like Shor or Grover that allow you to break cryptography or solve hard problems.
For electronic qubits, the largest number factored is “21”, through a real quantum circuit of 4 qubits done in 2012: Computing prime factors with a Josephson phase qubit quantum processor
For photonic qubits, the record for the largest number factored is “15”, also with 4 qubits, done in 2007: Demonstration of Shor's quantum factoring algorithm using photonic qubits
There has been zero progress since. Additionally, both these photonic and electronic qubit implementations of Shor's algorithm relied on prior knowledge of the factors. These demos used a compiled or semi-classical version of the algorithm, meaning they optimized the quantum circuit based on precomputed classical information about the solution. So, it essentially useless for computation, and was only meant to show ability of fine qubit control.
 |
|---|
| Excerpt from “Pretending to factor large numbers on a quantum computer” |
This is common in QC, because it's basically impossible to create any kind of real meaningful circuit that runs on actual, properly entangled qubits.
But I thought bigger numbers have been factored?
There are many other sources claiming that bigger numbers have been factored, like 143 or 56153, but this is often twisted into misleading nonsense by news articles. This is not Shor, these papers use either ising hamiltonian models or adiabatic quantum computing, which are processes closer to quantum annealing. They are converting the “factoring of the number” into an “optimization” problem, where the lowest energy state that the system settles to will automatically have the factor answer – but THESE ARE NOT GENERAL ALGORITHMS. It is not possible to use these algorithms to factor a private key that is 256 bits long. The bigger the number, the harder it is to encode into an optimization problem that fits an ising state – and eventually it becomes impossible as there's no way to map that solution into a (sensible) optimization problem. Below is an analogical visualization of the process.
 |
|---|
| An analogy for Adiabatic Quantum Computation. The image shows a “linear regression” process (finding the best-fit for a line, given a set of points). The strings are poked through the holes and tied to the rod and pulled tight. If the same pulling force is applied to each string, the balance from all the different tensions will make the rod “settle” into the best fit. This is essentially how adiabatic quantum computation works, but in higher dimensions. You want to find a set of “holes” (a state encoding) that when “pulled” (electrons settling into lowest energy state), will give your your best-fit solution (in this case, the factors of a large number). |
These quantum annealing adjacent processes exploit quantum effects, but they're not leveraging the full computation ability of entanglement. It's more like how you can solve a maze by feeding water into it, and the flow of water will naturally take the path of least resistance, so the path where the water flows strongest is the solution.
 |
|---|
| Water flow solving a maze (source) |
Full quantum computation through entangled states is a different mechanism. A universal quantum computer uses sequences of carefully controlled operations (gates) to manipulate the inner properties of the entire entangled quantum state. The machine can interfere and redirect amplitudes in that exponentially large “probability space,” effectively doing many computations at once and selectively reinforcing the right outcomes via quantum interference. Quantum annealers don't provide that kind of control, so they can't access the full exponential power hidden in an entangled system.
Misleading and meaningless “benchmarks”
Many other papers that use different “benchmarks” for achieving quantum computation breakthroughs are also misleading, like Google Willow which uses Random Circuit Sampling (RCS) as a benchmark – to basically have a quantum system that can sample its own state... and they state that this it does this a septillion times faster than a classical computer... but of course it does? These kinds of benchmarks are equivalent to saying the following:
Our new computer, which is an aquarium tank full of water that we shake, simulates fluid dynamics at a scale of 10^17 molecules a septillion times faster than if we were to try to simulate every particle in that whole aquarium tank on a classical computer
It's not computing anything. The aquarium tank, just like the quantum system doing RCS, is not a “simulator”, it's just the real thing evolving its state according to the laws of physics. Of course it's “faster” than simulation of the same set of particles inside software.
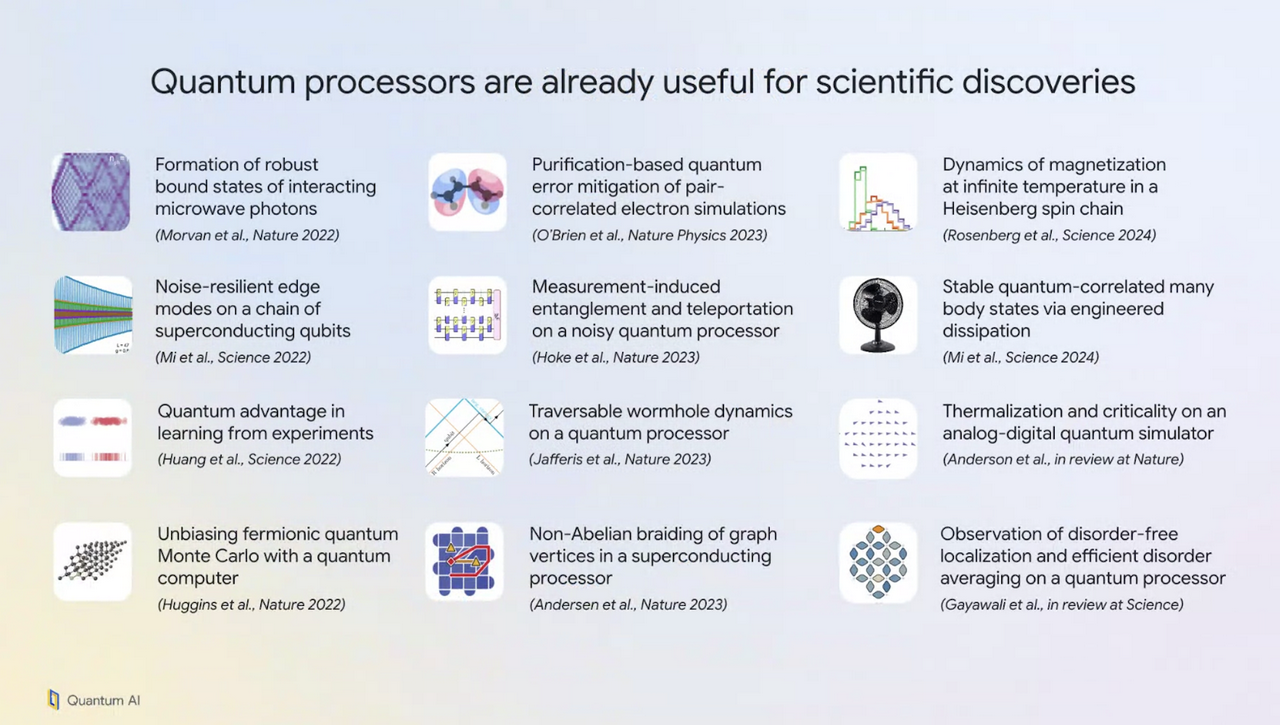 |
|---|
| You might notice that all the things that quantum computers are “claimed” to be useful for at the moment are physics related |
Although they're completely useless for computation, the ability of these systems to have fine-grained control over quantum states, electrons and photons, is useful for probing fundamental physics – as the image above shows. By creating precise entangled or semi-entangled systems, we can measure interactions and dynamics that are prohibitively complex through classical methods. It allows for exploration of exotic phases of matter, simulations of quantum field interactions, and the testing foundational principles of quantum mechanics in a setting with higher control and noise isolation than might be possible otherwise.
What about the new types of qubits?
Other claims, like those in Microsoft's paper on Majorana Zero Mode QC and the accompanying blog post of using “new physics” to create better qubits, border on intentional falsehoods. Microsoft has not found Majorana fermions[^1], and has not confirmed topological states of any sort. The only way to prove that they created a real Majorana Zero Mode state would have been to do a non-abelian braid operation (exchange of MZM states), and they did not do this, so it does not rule out alternative effects that merely mimic majorana signatures but that do not offer topological protection. Even if there was observation of some topological protection, scaling this design up to multi-qubit entanglement would likely destroy it regardless, since the Kitaev chain model used is too fragile to do so robustly with the given design.
 |
|---|
| An example of the egregious misrepresentation of a paper's results in the press release (paper left, blog right) |
The comportment of these companies when it comes to announcing their QC supremacy is reaching the point that it's indistinguishable from fraud. Microsoft has released a very similar paper on this before which they eventually had to retract from Nature: Authors retract Nature Majorana paper, apologize for “insufficient scientific rigour”
These kinds of approaches are in the “exotic quasiparticle” category, and scaling the creation of these stable quasiparticles substrates in a real system with crosstalk and actual functioning gates, rather than a toy setup that does nothing, is astronomically difficult. These are the “holy grail” because they avoid having to deal with quantum error correction, by providing topological protection from noise, but the approaches rely on novel, unproven or unsolved physics to actually work. If we could create and control these kinds of exotic quasiparticles at scale, the first step would not be quantum computing, rather we would already be using these techniques to make faster classical computers that leveraged spintronics or similar exotic physical effects that leverage quasiparticle fields (like with Quantum GPS).
It's important to note that even if we do solve topological qubit creation enough to actually enable non-trivial quantum computation, it does not solve the gate fidelity problem. In fact, in some ways it may make it even harder because topological states are very particular about how they want to move through a medium (or field) and interact with other particles. For example, in topological insulators created by strong spin-orbit coupling, particles will have very rigid paths as they move through electromagnetic fields – applying the desired transforms (which are also just modulation the same EM field) to this particle without causing it to break out of its topologically locked path is an extremely hard, unsolved problem, especially when you have to deal with spatial constraints of physical reality.
[1]: Even if the paper holds up, it's a kitaev chain model for 1D quasiparticle majorana fermions, so it's not “confirming” the existence of fundamental majorana fermions any more than Weyl Semimetals (which already experimentally support topological states) confirm the existence of Weyl Fermions
Claims of “improved algorithms”
There are many papers claiming that the quantum supremacy apocalypse moment will come “sooner” than expected now because of some new algorithm that can crack a bitcoin private key with “just” 50 million gates, but they are once again nonsense. They often mix the notion of physical and logical qubits, or in this case, assume a qubit gate fidelity, connectivity, and coherence time that is likely not physically realizable.
 |
|---|
| The quantum computer the algorithm in the paper requires to run. Getting >6 million qubits to link together reliably in this way is essentially impossible, as the section below on real scaling challenges will illustrate |
Usually these grand-claim papers rely on specialized arithmetic functions (e.g. quantum lookup tables, “clean” ancillas[^2], custom group arithmetic), and don't give a full uncomputation scheme or a complete space-time resource breakdown. It's easy to say “our modular multiplication is 2x faster”, but if that approach needs significantly more qubits or more complicated control logic, the gains disappear.
[2]: Support qubits that store “scratch” state used for enabling reversible computation
Large scale manufacturing of “Quantum hardware”
There are many low value press releases disguised as papers lately claiming that some company has been able to start mass manufacturing quantum computers, they are essentially all the same, with the same lies-by-omission, so I will just pick one and you can apply the same analysis to all of them.
As with all “progress reports” in this category, they focus heavily on component-level performance, but avoid system-level benchmarks because they have no ability to actually create a real quantum computer by linking together these components.
 |
|---|
| This illustration, like all the others in this paper (and all other papers of this nature), shows high fidelity across single-hops, with idealized examples of clean/trivial quantum states. They state “if in the simplest case, the photon actually makes it through, it does so with high fidelity” but omit information how many attempts are required to get one photon to make it through and actually be detected. This only gets worse with scale. |
For example, this is a photonics platform based on SFWM (Spontaneous Four-Wave Mixing). The paper handwaves away the unreliable nature of their photon sources. SFWM is inherently probabilistic, which means many attempts are needed to successfully generate the required photons. This interferes with actually linking these modules together in any meaningful way. There's some mention of BTO (Barium Titanate) electro-optic switches for multiplexing, but it's not enough to make any kind of meaningful computation possible.
Scaling this system requires immense resources across many verticals. FBQC (Fusion Based Quantum Computation) needs enormous numbers of photons, and there's no concrete estimates stated of how many physical components would be needed for practically useful algorithms.
In the next section, I'll use this paper as an example of how hard it would actually be to scale.
Scale of requirements for a real, useful quantum computer
If we do some rough math, for running Shor on a 256-bit ECC key (such as those used in bitcoin), we can see how ridiculous it gets. Shor requires at least 1,000 logical qubits to break such keys, so let's use that as the baseline.
For a realistic error rate, each logical qubit might require a code with distance ~15-25. Using a surface code or similar, this translates to ~1,000-2,500 physical qubits per logical qubit.
Each resource state preparation is probabilistic, success probability of fusion operations in the paper is ~99% for toy setups, but multiple attempts are needed per fusion operation in a real setup. As such, success probability per photon source is low (~1-10%). For reliable operation, system needs ~10-100x multiplexing.
So our requirements for this system are:
- 1,000 logical qubits × 2,000 physical qubits per logical qubit = 2,000,000 physical qubits
- Multiplexing overhead (10-100x): 20-200 million photon sources
- Number of detectors: Similar to number of sources, 20-200 million
- Number of switches and other optical components: Roughly 10x the number of sources, so 200 million to 2 billion
The chip in the paper has at most a few dozen active components (sources, detectors, switches). While for a real quantum computer, we need hundreds of millions to billions. That's 8-9 orders of magnitude from this proof of concept.
 |
|---|
| This is probably around the size of this photonics computer if you were to actually try to realize it with current technology (and probably still fail) |
That's not even counting the added complexity for the required control systems and needing to handle extremely fast and sophisticated classical feedback to keep up with the quantum error‐correction cycles, which would easily be another bottleneck (the system is bound by the “reaction limit”[^3]), or source of further instability, as it would be a huge amount of computation that would create heat and other noise, and is just an extremely non-trivial classical component with its own physics and engineering challenges that have not been solved at all at scale.
Manufacturing hundreds of millions to billions of these components with high yield / low defect rate, connecting them in a computationally useful way, and keeping signal loss & error rates from multiplying exponentially, while also having to keep the entire massive system at 2 kelvin, is not something humanity is capable of with our current technology and understanding of physics.
[3]: “Reaction limit” refers to the minimum runtime imposed by the need to measure qubits, process those measurement results classically (including error‐decoding), and then feed the outcome back into the quantum circuit. Many fault‐tolerant gates in a surface‐code architecture require this real‐time classical feedback to proceed. Even if the physical qubits and gates can operate at very high speed, no step that depends on measurement results can finish sooner than the classical processing latency. Thus, if the algorithm has a certain “reaction depth” (number of measurement‐and‐feedforward layers), and each layer requires (say) 10 µs of classical processing, then you cannot run the computation in under reaction_depth x 10 µs, no matter how fast the hardware otherwise is.
Conclusion
We are nowhere near being able to realize useful quantum computation. It is not coming in 10 or 20 years. If we have figured out how to create real, stable topological qubits in 10-20 years, the progress can start then. Until that point, you should disregard pretty much all news in this category.
Our current state of the art is as far off from real quantum computing, as using a magnifying glass and the sun to mark wood is to EUV lithography.